Worksheet A02d
6) log₅(log₃x)=log₁₀₀100
log₅(log₃x)=1
log₃x=5¹
x=3⁵
=243
7) log₅x=a log√5y=b
express xy² as a power of 5
x=5ª y=√5ᵇ
=5^b/2
xy²=5ª x 5^2b/2
=5^a+2b/2
=5^a+b
*Don't cancel your answer even if it seems wrong (sometimes it might be correct) only cancel after realising the mistake and redoing.
Worksheet A02e
9) 6ⁿ + 6^n+1 + 6^+2
= 6ⁿ+6ⁿ6+6ⁿ6²
= 6ⁿ(1+6+36)
= 6ⁿ(43)
∴divisible by 43 for all natural values of n.
11) log₅(5-4x) = log√5(2-x)
= log₅(2-x)/log₅5^1/2
= log₅(2-x)/(1/2)
= log₅(2-x)²
5-4x = (2-x)²
= 4 - 4x + x²
x²=1
x=±1
* Sorry for the late post
Thursday 28 February 2013
Tuesday 26 February 2013
Lesson Summary (February 26th 2013)
Morning Lesson:
We learnt how to solve logarithms using different methods.
Method 1: Covert log form to exponential form.
Method 2: Use change of base formula first.
For example:
Afternoon Lesson:
From the tables we have calculated out, we can conclude that:
- Power: loga (xp) = p loga x
- Product: loga (xy) = loga x + loga y
- Quotient: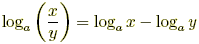
A formula can also be inputed into your graphic calculator to help change base:
Sorry I will input the formula when I get the paper back ><
Otherwise, you can use this log rule to change base too:
- Change of base formula:
http://www.mathwords.com/c/change_of_base_formula.htm
Things to take note:
We learnt how to solve logarithms using different methods.
Method 1: Covert log form to exponential form.
Method 2: Use change of base formula first.
For example:
Afternoon Lesson:
From the tables we have calculated out, we can conclude that:
- Power: loga (xp) = p loga x
- Product: loga (xy) = loga x + loga y
- Quotient:
A formula can also be inputed into your graphic calculator to help change base:
Sorry I will input the formula when I get the paper back ><
Otherwise, you can use this log rule to change base too:
- Change of base formula:
http://www.mathwords.com/c/change_of_base_formula.htm
Things to take note:
loga (x + y) ≠ loga x + loga y
loga (x – y) ≠ loga x – loga y
Wednesday 20 February 2013
Applications OF Exponential and Logarithm
APPLICATIONS:
OF EXPONENTIAL
GRAPHING EXPONENTIAL
====================================================
OF LOGARITHM
GRAPHING LOGARITHMS
====================================================
KEY RULES OF LOGARITHMS
====================================================
GUIDELINES TO SOLVE LOGARITHMS
TI84plus : Logarithms - Change of Base
TI84plus : Logarithms - Change of Base
How to use TI84 to Calculate Log of a different Base
How to Programme Change of Base
Tuesday 19 February 2013
Lesson Summary 19/2/2013: Wee Chang Han
Logarithm
Laws of Logarithm:
1.
a^x = y
is equals to:
log a(y) = x
2.
log10 = lg
log e = l(n), n = natural log.
3.
lg 1 = 0
log10 (1) = 0
10^0 = 1
Because:
loga(1) = 0
a ^0 = 1
where a ≠0.
4.
loga(a) = 1
where a ≠ 0, a >0
log10(10) = 1
because:
log10(10) = 1
10^1 = 10
Note:
5.
log10(-5) = error?
why?
-5 = 10^?
there is no value for the power of 10 to become -5, therefore log a base b = c, where a ≠ a negative integer or < 0.
6.
loga(b) = log10(b) / log10(a)
= ln(b) / ln(a)
caution!:
lg(b)/lg(a) ≠ b/a (do not cancel!!)
Correct:
lg(b)/ lg(a) = calculate both the top and the bottom.
7.
logc(ab) = logc(a) + logc(b)
8.
logc (a/b) = logc (a) - logc (b)
9.
log10(100) = log10(10)^2
= 2log10(10)
= 2
note:
loga(b)^n = n loga(b)
Friday 15 February 2013
Using TI 84Plus and simple programme
INTRODUCTION TO TI84 Plus
Programming QUADRATIC INTO TI84
Study the video provided for clarity of concept and greater appreciation of TI84plus.
Task 1: Simulate the programme into your TI84plus. Call it QUAD
Task 2: Extend your learning by considering the case when the answers are not Real ie. Imaginary
Thursday 14 February 2013
Lesson Summary 14/2/13 Ryan Tan
Surds
Important = *
*
(2√3)^2
=2√3 x 2√3
=4√3√3
=4(√3)^2
=4(3)
=12
Conjugate Surds
*
(a+b)(a-b) = a^2 - b^2
(√a+√b)(√a-√b)=(√a)^2-(√b)^2
(a^1/2 + b^1/2) (a^1/2 - b^1/2) = (a^1/2)^2 - (b^1/2)^2
2√3^2=
a) 2√3 √3 (correct)
b)2(√3)^2 (correct)
c)2 . 3^1/2x2 (correct)
d) 4(3) (wrong)
e) √4(3) ^2 (wrong)
f) √4 √9 (wrong)
To convert irrational surds into rational surds
By similar surd
1/√2 x √2(to both numerator and denominator)
= √2 /2
By conjugate surd
(1/ √3 - √2) x √3 + √2 (to both numerator and denominator)
=√3 + √2/ 3-2
=√3 + √2 / 1
Wednesday 13 February 2013
Tuesday 12 February 2013
Monday 11 February 2013
Friday 8 February 2013
Thursday 7 February 2013
Wednesday 6 February 2013
Lesson Summary 7/2/13 Shaun Ng
Level Test
Elementary math
Duration: 45 mins
30 marks
Topics:
- Algebraic manipulation
- Factorisation
- Expansion
- Algebraic Fraction
3 Indices (no surds + logs) (quiz c)
- Quadratic Function/graph plotting (U shaped and n shaped)
Additional math
Duration: 45 mins
30 marks
Topics:
- Polynomials
- Remainder Factor Theorem
- Cubic expression/equation
- Partial fraction
(All Jumbled up)
(Start doing Exam Prep Questions)
Question for fun
Given that the roots of a quadratic function is -3 and 1. Find the function if x=-3 (x+3)=0
- Case 1
the coefficient of x^2 is 2 (3)
- Case 2
y intercept is -6. (3)
Sketch the above function(s), showing clearly the x and y intercepts, and the turning point. State also the nature of turning point. (2)
y = f(x) = ax^2+bx+c
= A(x+d)(x+e)
= A(x_3)(x-1)
= A(x^2+2x-3)
=Ax^2+2Ax-3A
- f(x) = 2(x+3)(x-1)
= 2x^2+4x+6
- f(x) = A(x+3)(x-6)
x=0, f(0) = A(3)(-1) = -6
A = 2
Hence, f(x) = 2(x+3)(x-1)
= 2x^2+4x-6
Nature of turning point = Minimum tp
Turning point = Two x intercepts added/2
Sub x value into answer for a.]]]
Lesson Summary 6th Feb - Wednesday ; Kaelan
Practice 1,2,3,4 Answers:
Practice 1:
1 = A(x+2) + B(x+1)
1 = (A+B)x + 2A + B
Compare Co-efficients. A+B = 0
2A+B=1
Therefore: A = 1; B = -1
1 1
------ - ------
(x+1) (x+2)
b) Simple:
9x+9 9(x+1) 9
--------------- = ----------------- = --------
(x+1)(x-2) (x+1)(x-2) (x-2)
c) 3x+5 = A(x+2)(x+3) + B(x+1)(x+3) + C(x+1)(x+2)
Sub x = -1
2 = 2A
A = 1
Sub x = -2, -1 = -B, B = 1
Sub x = -3, -4 = 2C, C = -2
Therefore : 1 1 2
------------- + ------------- - ------------
(x+1) (x+2) (x+3)
Practice 2 :
1 = Ax(x-1) + B(x-1) + Cx^2 OR 1=(Ax+B)(x-1)+Cx^2
1 = (A+C)x^2 + (B-A)x -B OR x=1, C=1
Compare Coefficients OR x=0, B=-1
B=-1 OR x=-1, A = -1
A =-1
C = 1
A question :
x^2
------------------
9-x^2
Long divide to give : -1 + 9/9-x^2
= -1 + 9/(3+x)(3-x)
9 = A(3-x) + B(3+x)
x=3 , B=1.5
x=-3, A=1.5
-1 + 3/(6-2x) + 3/(6+2x)
NOTE: ALWAYS FACTORISE, A NON FACTORISED POLYNOMIAL WILL NOT WORK. have fun in a loop.
Tuesday 5 February 2013
Partial Fractions - Jia Qi and Carissa
Definition:
Partial fractions are used to simplify a complex fraction into two or more fractions. This is so that there will be less confusion when dealing with algebraic fractions.
Proper Rational Expression:
The degree of the top is less than the degree of the bottom
Improper Expression:
The degree of the top is greater than, or equal to the degree of the bottom.
Use polynomial long division first. The remainder will be the proper fraction, use the proper fraction to solve the question.
Workings:
Different cases will result in different partial fraction forms:
Lesson Summary 5th February
Homework :
Linoit
Comment on the posts on the math blog about the error
Prepare a thing plastic red file for filing .
Corrections
Remember :
Rules of index
Thanks to Justin
For Comparison
In order to rid the denominator of the surd/square root , we rationalize it .
Rationalizing is the process whereby we multiply the denominator by another fraction with the numerator and denominator like it . We make use of the identities such as : (a+b)^2 = a^2 + 2ab + b^2 ,
(a-b)^2 = a^2-2ab+b^2 or (a+b)(a-b) = a^2-b^2
Recall : Prime factorization
It is a way of breaking down a compound number into prime factors
Monday 4 February 2013
Lesson Summary ~(•O•)~ 4/2/13
RECALL:
~(•o•)~ Partial Fractions! Read through the summaries posted by yourself/others~(•o•)~ Level Tests are on Week 7 & 8, starting mugging.
HOMEWORK:
~(•o•)~ Check what you haven't done on the homework spreadsheet.
~(•o•)~ AceLearning for those who did badly on the various quizzes and tests.
~(•o•)~ Assignment 01 and 02 are now due on Friday~!
REVISE:
~(•o•)~ The 9 laws of indices: (here's a helpful table)
Please remember to fully revise all laws as they will be used in Indices and Surds.
LESSON:
~(•o•)~ Indices and Surds: Forms
Surd Form: When the base has a squareroot with it (√5)
Radical Form: When the base has an fractional index (2^(2/123))
~(•o•)~ Indices and Surds: Rationalization
Rationalization is the act of eliminating the squareroot (√x) from the denominator.
BACK TO BASICS– " 1/2 VS 1/3"
How do we determine which is bigger?
We change make them have an equal denominator. Thus, the LCM between 2 and 3 is 6. Therefore, we multiply 1/2 with 3/3 (Note how this is 1 whole), and 1/3 with 2/2. Eventually, we get "3/6 > 2/6"
ON TO SURDS! – "1/2 VS 1/√2"
How do we determine which is bigger?
Once again, we change them to make them have an equal denominator. In this case, we change the denominator to 2. As the first fraction already has a denominator of 2, we will work with 1/√2.
2 divided by √2 is √2. Thus, we multiply 1/√2 by √2/√2 (1 whole), and get √2/2.
Therefore, we would get "1/2 < √2/2"
Rationalizing with a^2 - b^2 – "1/(3 - 2) VS 1/(√3 - √2)"
To rid of the surd denominator, we use the 'a^2 b^2 = (a + b)(a - b)' concept.
In this scenario, our denominator is (√3 - √2) which is our (a - b). Thus, to rid of it, we multiply it by (√3 + √2) which represents our (a + b).
Thus, we multiply 1/(√3 - √2) by (√3 + √2)/(√3 - √2) <-- which is one whole!
This gives us (√3 + √2)/(3 - 2) = (√3 + √2)/1
Therefore, "1 < (√3 + √2)"
TASK FOR 5th February 2013
TASK FOR 5th February 2013
Period 1
1. Self Assessment ( please refer to Quiz C [10mins]
- complete the corrections
- identify the errors committed be it (i) conceptual or (ii) carelessness
2. Collaborative Effort - via Maths Blog - Linoit exercise [20mins]
- S3-05 complete the portion on Indices
- S3-09 complete the portion on Surds
3. Peer Assessment - via Maths Blog activity
- INDICES & SURDS - The Mistake Fragment part 1
- post the responses as comments
4. Self Assessment - via Maths Blog activity
- INDICES & SURDS - The Mistake Fragment part 2
- post your responses as comments
================================================================Period 2
5. Diagnostic Test 2 - Indices, Surds and Logarithms
- do be done on foolscap papers
- scribe of day to collect and past to teacher
Period 1
1. Self Assessment ( please refer to Quiz C [10mins]
- complete the corrections
- identify the errors committed be it (i) conceptual or (ii) carelessness
2. Collaborative Effort - via Maths Blog - Linoit exercise [20mins]
- S3-05 complete the portion on Indices
- S3-09 complete the portion on Surds
3. Peer Assessment - via Maths Blog activity
- INDICES & SURDS - The Mistake Fragment part 1
- post the responses as comments
4. Self Assessment - via Maths Blog activity
- INDICES & SURDS - The Mistake Fragment part 2
- post your responses as comments
================================================================Period 2
5. Diagnostic Test 2 - Indices, Surds and Logarithms
- do be done on foolscap papers
- scribe of day to collect and past to teacher
INDICES & SURDS - The Mistake Fragment 2
By Mr Johari
Identify the mistakes shown below and post your corrections.
For the correction identify the correct rules.
Find the algebra mistake:
1.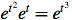
2.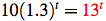
3.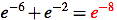
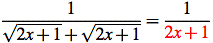
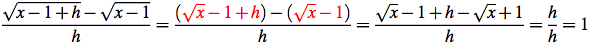
Identify the mistakes shown below and post your corrections.
For the correction identify the correct rules.
Find the algebra mistake:
1.
2.
3.
4. Find the algebra mistake:
5. Find the algebra mistake:
INDICES & SURDS - The Mistake Fragment part 1
BY MR JOHARI
Context
Below shown the solution posted by the secondary 3 students during the 4th February 2013 Maths Quiz C.
There are errors in the solution posted.
Focus
Error Analysis and Peer Evaluation
Individual Effort
Task
You are required to post the following as a comment:
(i) Nature of error - conceptual or carelessness (be very specific in your description)
example - careless error due to arithmetic (addition)
example - conceptual error due to error in (a + b)^2 = a^2 + b^2.
(2) Correction to the error
Ensure that your solution is concise and correct.
Sunday 3 February 2013
INDICES, SURDS & LOGARITHMS
BY MR JOHARI
This is an Interclass Collaboration on INDICES and SURDS
S3-05 focuses on INDICES
S3-09 focuses on SURDS
TASK
1. Identify as many laws of Indices as possible.
2. Include condition, where possible such as a > 0.
3. Include also examples on how the rules are used.
CLICK
Indices and Surds to access Linoit
CLICK
Saturday 2 February 2013
Lesson Summary(25/1/13) / Partial Fractions summary(Lee Kai En)
Terms
Proper Fraction - A fraction where the numerator < denominator
Improper Fraction - A fraction where the numerator > denominator
Proper Algebraic Fraction - A fraction where the degree of the numerator < degree of the denominator
Improper Algebraic Fraction - A fraction where the degree of the numerator > degree of denominator
What is partial fraction?
Partial fraction is the breaking up of a fraction to find the original parts of the fraction which will add up to give the final simplified expression.
Improper Fraction - A fraction where the numerator > denominator
Proper Algebraic Fraction - A fraction where the degree of the numerator < degree of the denominator
Improper Algebraic Fraction - A fraction where the degree of the numerator > degree of denominator
What is partial fraction?
Partial fraction is the breaking up of a fraction to find the original parts of the fraction which will add up to give the final simplified expression.
Methods of finding partial fractions
Method 1: Decomposition
E.G.
Method 1: Decomposition
E.G.
Step 1: Factorise denominator first
Step 2: Split the fraction up.
Step 3: Make it such that the denominators "disappear"
Methods of solving
Method 1: Comparing coeffs.
E.G. 3x+5 = (2A+B)x + (A-3B)
2A+B = 3
A-3B = 5
.......simultaneous equation.......
Method 2: Substitution
E.G 3x+5 ≡ A(2x+1)+B(x-3)
if x = 3, A = 2
*(A can be found much easily)
if x =
After finding the values of the unknown(such as A and B), substitute in the values into the fractions and express it as a partial fraction.
E.G.
Subscribe to:
Posts (Atom)
.jpeg)
.jpeg)











.JPG)























.gif)






