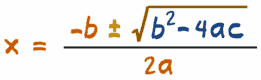Lesson summary 26/3 Shaun Ng

Quadratic inequalities: 

Step 1: Find roots (by factorising)

Step 2: Sketch and include x-intercept (roots)

Step 3: Check sign, <0 answer is part below x-axis

           >0 above x axis

Practice QNs Answers p26 - p29 below

Result Analysis - Lee Kai En(10)

Commands used:

To Convert to % --> x/total score*100

To Convert to Grade --> Vlookup

To Analyse --> Countif

Result Analysis - Owen Ong (15)

Lesson Summary 13/3/13 Mason Sim_12

Practice 10 Page 158
Show that the equation x^2+(k+1)x+k=0 has real roots for all values of k .

Practice 12 Page 159
Show that the roots of the equation x^2-2x-p+2=0 are real and distinct if p>1 

Practice 15 Page 162

That should be all for todays lesson 

12/3 Math Scribe Post – Justin (11)

What we did today ~(•0•)~ 
- Quiz on laws of surds, logs, indices, and some log questions below
We did this to revise our concepts as it is important to understand the laws before we can manipulate them. Also because logs are fun. 

- Diagnostic Test on Quadratic Equations
To revise and re-emphasize on what are the key concepts in this topic. Also because quadratic is fun. 

- Peer Assessment 
This taught us how to improve our answers, in terms of mathematical concepts, explanations and presentation.
Presentation will ultimately affect your explanation, which then affects your mathematical concept which is a shown in your presentation. It's a vicious cycle. 
Through this cycle, we learn that we communicate with the reader when writing out math equations. We must explain what we're doing in the question well, or else it won't make any sense. This form of communication is key in exams. 

Mathematical concepts we learnt today ~(•0•)~ 
MISCONCEPTIONS: (reasons for our tests)
a^(-n) = a^(1/n) 
This is wrong as when the power is negative, your base is now a denominator, not your power. 
Make sure to get your concepts down for the exam, for they are our foundation! ^^

CONCEPTS: 
x + 1 = 0 
This is an equation. It shows that both sides are of the same value.
x + 1 > 0 
This is an inequality, it shows in the inequality between both sides in terms of value.
x + 1 
This is an expression, of not needed to be solved but rather simplified. 

Quadratic - Part 2 Peer Assessment

by Mr Johari

This is a followup to the individual assessment activity on Quadratic. 

• In this activity you are required to assess the work done by your peers.
• This is an individual effort.
• Each student will be required to assess only 2 questions as shown in the chart below.
• Objectively you are not allowed to assess your own work.
• The criteria for assessment is shown in table 2. (no grading required, the rubric serves as a guide for you)

Method of Assessment

• Read the question carefully. Highlight key terms or words such as evaluate, expand, simplify, prove etc.
• Review the solution done by your peers. Use the following guiding questions
• Is the Mathematical Concept sound? Is there evident that the student understands the concept (through the working/process shown)
• Do you understand the explanation given without any doubts?
• Is the process clearly shown?
• Is the process well organised and easy to follow?
• Does the answer make sense? 

• Post as Comment (under the question(s) assigned the following:
• Your thoughts on the following
• clarity of mathematical concept as required by the question (if there is ambiguity or lack of clarity state why example: the sum of roots is not clearly defined or the final answer does not take into consideration that a>0 etc)
• clarity of explanation/process (example: the working is not explicitly shown, it is difficult to understand, explanation is succinct and easy to follow and comprehend)
• organisation of answer (example: the answer is clear and takes into consideration of the conditions stated in question such as a>0, the organisation is weak and very vague, some important steps are skipped etc)

Table 1

Table 2

Quadratic - Practice 8 (Carissa)

Show that the equation a^2x^2 + 3ax + 2 = 0 always has real roots.

From the equation we know the values of a, b, c.

The discriminant (D) determines the roots of an equation.

if D > 0, the roots are real and distinct

if D = 0, the roots are real and equal

if D < 0, the roots are imaginary

Substituting the values of a,b,c into b^2 - 4ac, we are able to find the value of the discriminant.
a^2 is always more than 0.
Since the value of the discriminant for a^2x^2 + 3ax + 2 is more than 0, we know that its roots are real.

Quadratic - Practice 6 (Ryan)

Quadratic - Practice 10 (Shaun Ng)

Quadratic - Practice 9 (Denzel)

Practice 9

Find the value of k such that the equation x^2+kx+2k-3=0 has only one real root.

Quadratic - Practice 7 (Desiree)

Quadratic - Practice 13 (Farrell Nah)

Quadratic - Practice 14 (Justin)

Results Analysis - Wee Chang Han, Register 20

Quadratic ... in a nutshell

by Mr Johari
Source: http://perfectmaths.com/quadratic-equations/

ICT Task - Score Analysis using Numbers

by Mr johari

This is how the final table should look like.
It should contain the following information:

1. Table of values (score, Percentage, Grade)
2. Analysis (that automatically counts the number of students getting the various grades from A1 to F9) (the table in yellow highlights the category of score from A1 - F9)
3. mean subject grade (MSG), mean marks from column 2, Total number of candidates, Highest Score and Lowest Score - tabulated from column 2)
4. Visual representation in the form of a bar chart.

Your task: 

complete the table and the following students please post a link to your table.

index # 5, #10, #15, #20.

Lesson Summary: 6/3/13 NUMBERS!!!

To Do:
- Be prepared for performance task
- Play around with numbers

Here is my version of the file we did today: http://www.mediafire.com/?hm3e2dkqua1krm7

Lesson Summary 5 March

Steps (shortcut) to sketching ><

1) if a is positive, the graph has a min turning point
 if a is negative, the graph has a max turning point

2) c refers to the y intercept of the graph

3) D, the discriminant, affects the nature of the roots
if D is greater than zero, the roots are real and different
if D is equal to zero, the roots are real and similar
if D is less than zero, the roots are imaginary

4) in completing the square [ (x+h)^2+k ], the turning point is (h,k)

eg. y=x^2-3x+5
1) is a graph with a min turning point
2) has a y intercept of 5
3) is imaginary (D=-11)
4) has a turning point of (1.5, 2.75)

___________________________________________________________
Difference between plotting and sketching

                     Drawing/Plotting                 SKetching
Scale                       Y                               N
Accuracy                  Y                               N
Plotting Points            Y                               N
Label                       Y                               Y
Construction lines       Y                               N

Lesson Summary

Quadratic

-graph(parabola)
one turning point
line of symmetry( (X1+X2)/2 )
intercept to y ( c of y=ax^2+bx+c)
intercept to x  (X1 X2)
(a determine its shape)


-
(a+b)^2=a^2+2ab+b^2
a^2-b^2=(a+b)(a-b)


-function
(base on a vertical line test) <many to one>
basic form: ax^2+bx+c=0
roots:
    discriminant: D=b^2-4a
    D>0, real & different roots
    D=0, real & equal
    D<0, imaginary(complex root)
solving:
    cross method
    formula: x= ( -b+(-)√D )/ (2a)
    


sum of roots: -b/a
product of roots: c/a

x^2-(-b/a)x+c/a=0
x^2-(X1+X2)x+X1X2=0
x^2-(sum of roots)x+product of roots=0

Lesson summary 3.1

Discriminant table

Sorry for posting late:P
 Crystal

REAL LIFE APPLICATION OF QUADRATIC EQUATION

by Mr Johari

source: http://www.mathsisfun.com/algebra/quadratic-equation-real-world.html 

REAL LIFE APPLICATION OF QUADRATIC EQUATION

EXAMPLE 1

Balls, Arrows, Missiles and Stones If you throw a ball (or shoot an arrow, fire a missile or throw a stone) it will go up into the air, slowing down as it goes, then come down again ... ... and a Quadratic Equation tells you where it will be! Example: Throwing a Ball A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. When does it hit the ground?

Ignoring air resistance, we can work out its height by adding up these three things:

The height starts at 3 m:		3
It travels upwards at 14 meters per second (14 m/s):		14t
Gravity pulls it down, changing its speed by about 5 m/s per second (5 m/s2):		-5t2
(Note for the enthusiastic: the -5t2 comes from -½at2 with a=9.81 m/s2)

Add them up and the height h at any time t is:

h = 3 + 14t - 5t²

And the ball will hit the ground when the height is zero:

3 + 14t - 5t² = 0

Which is a Quadratic Equation ! In "Standard Form" it looks like:

-5t² + 14t + 3 = 0

Let us solve it ...

There are many ways to solve it, here we will use the factoring method:

Will be easier if we multiply all terms by -1:		5t2 - 14t - 3 = 0
Now our job is to factor it. We will use the "Find two numbers that multiply to give a×c, and add to give b" method in Factoring Quadratics. a×c = -15, and b = -14. The positive factors of -15 are 1, 3, 5, 15, and one of the factors has to be negative. By trying a few we find that -15 and 1 work (-15×1=-15, and -15+1= -14)
Rewrite middle with -15 and 1:		5t2 - 15t + t - 3= 0
Factor first two and last two:		5t(t - 3) + 1(t - 3) = 0
Common Factor is (t - 3):		(5t + 1)(t - 3) = 0
And the two solutions are:		5t + 1 = 0 or t - 3 = 0
		t = -0.2 or t = 3

The "t = -0.2" is a negative time, impossible in our case.

The "t = 3" is the answer we want:

The ball hits the ground after 3 seconds!

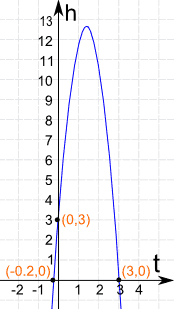Here is the graph of the Parabola h = -5t2 + 14t + 3 It shows you the height of the ball vs time Some interesting points: (0,3) When t=0 (at the start) the ball is at 3 m (-0.2,0) Says that -0.2 seconds BEFORE we threw the ball it was at ground level ... this never happened, so our common sense says to ignore it! (3,0) Says that at 3 seconds the ball is at ground level. Note also that the ball reaches nearly 13 meters high.

Note for the enthusiastic: You can find exactly where the top point is! The method is explained in Graphing Quadratic Equations, and has two steps:

Find where (along the horizontal axis) the top occurs using -b/2a:

• t = -b/2a = -(-14)/(2 × 5) = 14/10 = 1.4 seconds

Then find the height using that value (1.4)

• h = -5t² + 14t + 3 = -5(1.4)² + 14 × 1.4 + 3 = 12.8 meters

So the ball reaches the highest point of 12.8 meters after 1.4 seconds.

===========================================================

EXAMPLE 2

Example: New Sports Bike

You have designed a new style of sports bicycle! Now you want to make lots of them and sell them for profit.

Your costs are going to be:

• $700,000 for manufacturing set-up costs, advertising, etc
• $110 to make each bike

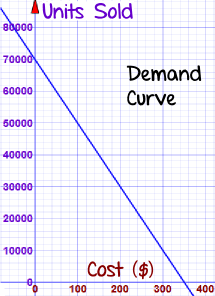
Based on similar bikes, you can expect sales to follow this "Demand Curve": Unit Sales = 70,000 - 200P Where "P" is the price. For example, if you set the price: at $0, you would just give away 70,000 bikes at $350, you would not sell any bikes at all. at $300 you might sell 70,000 - 200×300 = 10,000 bikes

So ... what is the best price? And how many should you make?

Let us make some equations!

How many you sell depends on price, so use "P" for Price as the variable

• Unit Sales = 70,000 - 200P
• Sales in Dollars = Units × Price = (70,000 - 200P) × P = 70,000P - 200P²
• Costs = 700,000 + 110 x (70,000 - 200P) = 700,000 + 7,700,000 - 22,000P = 8,400,000 - 22,000P
• Profit = Sales-Costs = 70,000P - 200P² - (8,400,000 - 22,000P) = -200P² + 92,000P - 8,400,000

Profit = -200P² + 92,000P - 8,400,000

Yes, a Quadratic Equation. Let us solve this one by Completing the Square.

Solve: -200P² + 92,000P - 8,400,000 = 0

Step 1 Divide all terms by -200

P² – 460P + 42000 = 0

Step 2 Move the number term to the right side of the equation:

P² – 460P = -42000

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2)² = (-460/2)² = (-230)² = 52900

P² – 460P + 52900 = -42000 + 52900

(P – 230)² = 10900

Step 4 Take the square root on both sides of the equation:

P – 230 = ±√10900 = ±104 (to nearest whole number)

Step 5 Subtract (-230) from both sides (in other words, add 230):

P = 230 ± 104 = 126 or 334

What does that tell us? It says that the profit will be ZERO when the Price is $126 or $334

But we want to know the maximum profit, don't we?

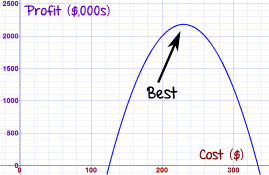
It will be exactly half way in-between! At $230

And here is the graph: Profit = -200P2 + 92,000P - 8,400,000 The optimum sale price is $230, and you can expect: Unit Sales = 70,000 - 200 x 230 = 24,000 Sales in Dollars = $230 x 24,000 = $5,520,000 Costs = 700,000 + $110 x 24,000 = $3,340,000 Profit = $5,520,000 - $3,340,000 = $2,180,000

A very profitable venture.

===========================================================

EXAMPLE 3

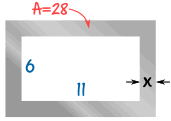
 Example: Small Steel Frame

Your company is going to make frames as part of a new product they are launching. The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm2 The inside of the frame has to be 11 cm by 6 cm What should the width x of the metal be?

Area of steel before cutting:

Area = (11 + 2x) × (6 + 2x) cm²

Area = 66 + 22x + 12x + 4x²

Area = 4x² + 34x + 66

Area of steel after cutting out the 11 × 6 middle:

Area = 4x² + 34x + 66 - 66

Area = 4x² + 34x

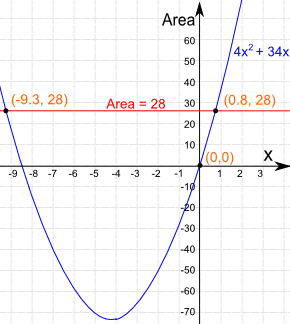
Let us solve this one graphically! Here is the graph of 4x2 + 34x : The required area of 28 is shown as a horizontal line. The area equals 28 cm2 when: x is approximately -9.3 or 0.8 The negative value of x make no sense, so the answer is: x = 0.8 cm (approx.)

===========================================================

EXAMPLE 4

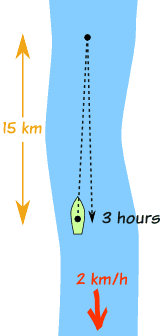
Example: River Cruise

A 3 hour river cruise goes 15 km upstream and then back again. The river has a current of 2 km an hour. What is the boat's speed and how long was the upstream journey?

There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land: Let x = the boat's speed in the water (km/h) Let v = the speed relative to the land (km/h) Because the river flows downstream at 2 km/h: when going upstream, v = x-2 (its speed is reduced by 2 km/h) when going downstream, v = x+2 (its speed is increased by 2 km/h) We can turn those speeds into times using: time = distance / speed (if you travel 8 km at 4 km/h it would take 8/4 = 2 hours, right?)

And we know the total time is 3 hours:

total time = time upstream + time downstream = 3 hours

Put all that together:

total time = 15/(x-2) + 15/(x+2) = 3 hours

Now we use our algebra skills to solve for "x".

First, get rid of the fractions by multiplying through by (x-2)(x+2):

3(x-2)(x+2) = 15(x+2) + 15(x-2)

Expand everything:

3(x²-4) = 15x+30 + 15x-30

Bring everything to the left and simplify:

3x² - 30x - 12 = 0

It is a Quadratic Equation! Let us solve it using the Quadratic Formula:

Where a, b and c are from the
Quadratic Equation in "Standard Form": ax² + bx + c = 0

Solve 3x² - 30x - 12 = 0

Coefficients are:		a = 3, b = -30 and c = -12
Quadratic Formula:		x = [ -b ± √(b2-4ac) ] / 2a
Put in a, b and c:		x = [ -(-30) ± √((-30)2-4×3×(-12)) ] / (2×3)
Solve:		x = [ 30 ± √(900+144) ] / 6
		x = [ 30 ± √(1044) ] / 6
		x = ( 30 ± 32.31 ) / 6
		x = -0.39 or 10.39

Answer: x = -0.39 or 10.39 (to 2 decimal places)

x =-0.39 makes no sense for this real world problem, but x = 10.39 is just perfect!

Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)

And hence the upstream journey = 15 / (10.39-2) = 1.79 hours = 1 hour 47min

And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min

Relation Between Roots & Coefficients of Quadratic Equation

by Mr Johari
source: http://www.tutorsonnet.com/math_homework_help/quadratic_equations

Knowing the Quadratic Equation

Part1:  Looking into the Roots and Coefficients of a Quadratic Equation

Part2:  Working backword - how to form a Quadratic Equation if you know the roots.

Revision : Solving Quadratic Equations

by Mr Johari
source: http://www.regentsprep.org/Regents/math

Let us review what has been done in previous 2 years.