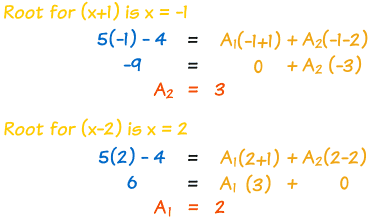STATUS OF WORK TO DATE

BY Mr Johari

This is the latest record of assignments, tasks and assessment.

Appreciate if you could check for assignments marked 'not submitted'..

As we are working towards realising your dreams of achieving distinctions in Maths - you have to do your part in monitoring your own progression.

However, if you are not able to manage yourself then we would collaborate with your parents to assist you.

ACE LEARNING ON-LINE QUIZ

by Mr Johari

To date only the following students have attempted the on-line Quiz(es) - Quiz 1-3.

Much appreciate their Committed and Courage in building their Confidence in the subject. It speaks volume about their Performance Character.

For others, I am sure you have a VALID reason for not attempting and a lack of commitment is surely NOT one of them.

Do let me know should you have problem accessing the ACE Learning portal.

Partial fractions summary (Shaun Ng)

Intro:  Partial fractions

- Instead of simplifying two fractions into one, we want to break them up here.
- Degree is the highest power of x in the set
- Proper fractions = Numerator < Denominator
- Improper fractions = Numerator > Denominator
- Proper algebraic fractions = Degree of numerator < Degree of Denominator
- Improper algebraic fractions = Degree of numerator > Degree of Denominator

Simplifying:

Previously we have been taught how to simplify two fractions into one. (/ sign = border between numerator and denominator)
For example:

8/x+9 + 2/x-3

1st step: Change denominator to the same thing, to do this multiple both numerator and denominator by the denominator in the fraction it is added or subtracted to.

8x-24/(x+9)(x-3) + 2x+18/(x+9)(x-3)

2nd step: Add or subtract the fractions together, by adding the numerators into one fraction.

10x-6/(x+9)(x-3)

This is the answer if we simplify.

Decomposition:

Now lets try something new using the same equation from example of simplifying.

10x-6/(x+9)(x-3)

1st step: Separate into two different fractions with a variable as numerator.

A1/x+9 + A2/x-3

2nd step: Multiply through the bottom to eliminate denominator

A1(x-3) + A2(x+9)

3rd step: Bring the 10x+6 in

10x+6 = A1(x-3) + A2(x+9)

4th step: Find the roots, so that we can eliminate 1 variable and find the other

Root for x-3 is 3
Root for x+9 is -9

5th step: Sub in and solve

Let x be 3
10(3) + 6 = A1(3-3) + A2(3+9)
36 = A2(12)
A2 = 3

Let x be -9
10(-9) + 6 = A1(-9-3) + 3(-9+9)
-96 = A1(-12)
A1 = 8

Hence, A1 = 8 and A2 = 3

6th step: Express as partial fraction

8/x+9 + 3/x-3

PARTIAL FRACTION - summary

BY MR JOHARI

PARTIAL FRACTION 

SUMMARY OF TYPES AS GUIDE

Source: ACE Learning

 

Other Source for reference: http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-partialfractions-2009-1.pdf

LESSON SUMMARY :D:D:D:D:DD:D

Heres what we've covered in class today...

1): Please do remember to organize your workings and provide necessary explanation otherwise the marker would not understand your concept.

2) FRACTIONS: What is a fraction?

A fraction is numerical quantity that is not a whole number 

Numerator/ Denominator

Whole Number- Both values of the numerator and the denominator are equal.

Improper Fraction-  The degree of the unknown in the numerator is higher than the denominator it is said to be a improper fraction 

Proper Fraction– The degree of the unknown in the numerator is lower than the denominator it is said to be a proper fraction.However, if the both the degrees are the same, it would NOT be a proper fraction

3)PARTIAL FRACTIONS

Definition: Partial fraction is breaking apart the final expression into its initial polynomial fractions.

How to solve a Partial Fraction:

Step 1: Factorising the denominator

Step 2: Separate

Step 3: Multiply through by the bottom so there no longer will be fractions

Step 4: Find the constant

Express it as a partial fraction

Summary on Partial fractions ( Mason Sim )

Partial fractions are a way of simplifying fractions that have polynomials in them into simpler , partial fractions , hence the name .  We break fractions into partials fractions so that we can handle them easier with less confusion .

Methods to solve partial fractions 
- Before starting , make sure that the fractions you have are proper ( Numerator degree is smaller than denominator degree. ) If the fraction is improper , use long division or synthetic division in order to get a mixed fraction . In order to make this into mixed fractions , we take the numerator divided by the denominator .

1) Decomposition 
- We factorize the denominator and break it up into factors
-We put different unknowns onto each denominator .
- Therefore , our partial fractions are equal to our original fraction
- Multiply the partial fraction side with the denominator
   >>>
- Start solving it like a normal equation
 ~ You can substitute the x values with those of the denominator such that it will equal 0 such as 2 or -1 in the example shown .



Table

Partial Fractions Summary - Kaelan

Partial Fractions:

Definition: The parts/components of a fraction in proper form of a factorable denominator that when added equal to the original fraction

Methods of solving

Finding the partial fractions (decomposing) of a fraction is the reverse operation of adding its factors.

BUT FIRST

If the degree of numerator is higher than the denominator, take it literally and divide fraction by long division. Then decompose the remainder.

1) Factorise denominator and put equals sign

2) Write a separate fraction for each factor on the RHS as the denominator.
-The numerator is the degree n of the denominator -1
-eg. numerator for linear (x+1) is a constant A -> A/x+1. numerator for quadratic is linear Bx+C...

3) For repeating factors, (x+1)^6. write a separate fraction for  x+1 , (x+1)^2, (x+1)^3 ...

4) Cross multiply numerators on RHS and remove the denominators on both sides.

5) Either compare coefficients or substitute values of x to find the unknowns A,B,C... 

6) Substitute / Rewrite partial fractions with the correct numerator 

                           

Summary on Partial Fractions - Ryan

Partial Fractions: To change an algebraic fraction into 2 separate fractions.

"A rational function which may be expressed as a sum of separate fractions is said to be resolved into its partial fractions."

There are different methods to deal with Proper fractions or Improper fractions

A Proper fraction is a fraction whose numerator is smaller than its denominator.

An Improper fraction is a fraction whose numerator is larger than its denominator.

If the rational function is a proper fraction:
For every linear or quadratic factor there is a corresponding partial fraction.
For every repeated linear factor there are 2 corresponding partial fractions.

To find the unknown constants you can:
compare coefficients
substitution method


If the rational function is an improper fraction:

You must divide it to obtain a quotient and a proper fraction so you can change the proper fraction into partial fraction form.

Partial Fractions- Jemima and Desiree

Partial Fractions

Partial fractions is a way of "breaking apart" fractions with polynomials in them.

Why do we want to do this?
Because the partial fractions are each simpler. This may be a very important step in solving the more complicated fraction.



Partial Fraction Decomposition
Step 1: Factorise the denominator
Step 2: Write one partial fraction for each of the factors
Step 3: Cross multiple so that there are no more fractions
Step 4: Find the constant

It only works for Proper Rational Expressions, where the degree of the top is less than the bottom.

The degree is the largest exponent the variable has.

Type of Fractions:
Proper: the degree of the top is less than the degree of the bottom.
Improper: the degree of the top is greater than, or equal to, the degree of the bottom.


If your expression is improper, then do Polynomial long division first. Obtain the proper fraction (e.g the remainder), then resolve the proper fraction into partial fraction.

Summary on Partial Fractions – Justin

PARTIAL FRACTIONS

Objective: To simplify algebraic fractions into two separate fractions, or a sum of a polynomial and a fraction. 

Types of Fractions:

Not in partial form

Improper– Where the highest power of the unknown in the numerator is higher than that of the denominator. If the powers are the same, the numerator's coefficient of the power with the highest unknown would be higher than that of the denominator.

Proper – Where the highest power of the unknown in the numerator is less than that of the denominator. If both highest powers are equal, the coefficient of the numerator's unknown with the highest power is less than that of the denominator.

In Partial form

'Mixed Fraction' – If the fraction is improper, we must represent it as the sum of a polynomial and a fraction. Thus we have to first use long division, with the denominator as the divisor, to divide the numerator and obtain our polynomial/whole number. 
The remainder would then have to be separated as well. 

Partial Fraction – "Taking apart one algebraic fraction with a quadratic denominator into two separate fractions, often with a linear denominator." 

How to represent fractions as partial fractions:

23 Jan Lesson Summary

Mr Johari's Interesting question...


(a) Solve the equation 2x^3 - 7x^2 - 7x + 30 = 0

2x^3 - 7x^2 - 7x + 30 = 0

(x + 2)(2x - 5)(x - 3) = 0

x = -2 or 3 or 2.5


(b) When the expression x^2 + bx + c is divided by x-2, the remainder is R. When the expression is divided by x+1, the remainder is also R

(i) Find the value of b

let f(x) = x^2 + bx + c

f(2) = f(-1)

4 + 2b + c = 1 - b + c

b = -1


(ii) When the expression is divided by x-4, the remainder is 2R. Find the value of c and R

f(4) = 2f(2)

16 + 4b + c = 2(2 + 2b + c)

sub b

16 - 4 + c = 2(4 - 2 + c)

c = 8

R = f(2) = (4 - 2 + 8) = 10

(iii) When the equation is divided by x-t, the remainder is 5R. Find the two possible values of t

f(t) = 5 x 10

t^2 + tb + c = 50

t^2 - t + 8 = 50

t = 7 or -6

(c)

the sketch shows part of the graph y = x^3+px^2+qx+r where p, q, and r are constants.
The points A, B, and C have co-ordinates (-2,0), (2,0) and (4,0) respectively.
Find p, q, r

let f(x) = x^3 + px^2 + qx + r

f(-2) = 0

f(2) = 0

f(4) = 0

Therefore: f(x) = (x + 2)(x - 2)(x - 4)
f(x) = x^3 - 4x^2 - 4x + 16

comparing coef.

-4x^2 = px^2
p = -4

-4x = qx
q = -4

r = 16

GRAPHIC CALCULATOR SALE (THU)

Graphic Calculator TI84plus

All sec 3 students will be required to buy TI84plus.

estimated cost - $158 

Vendor will be coming on 24 January 2013.

Time: 2 -3 pm (Canteen)
If payment is by cheque, please make it payable to "Learning Interactive Pte Ltd"

You may also purchase the calculator directly from Texas Instrument.

For Students on Financial Assistance please email Mr Ingham.

===================================================================================

LEVEL TEST 1

WK 7/8

AM AND MD

2 PAPERS - 30 MARKS EACH

22 Jan lesson summary

Quiz B Answers
1)
The expression (3x^3 + x^2 + ax - 5) has the same remainder when divided by (x-1) and by (x+2). Evaluate a and hence find the remainder when the expression is divided by (x-2).

ANS: f(x) = 3x^3 + x^2 + ax -5
if (x-1) = 0, x = 1
if (x+2) = 0, x=-2

Let f(1) = a-1
Let f(-2) = -2a-25

hence (a-1) = (-2a-25)
a=-8

if (x-2) = 0, x=2

Let f(2) = 7

2)
The expression [f(x) = ax^3 - 9x^2 + 7x + b] leaves a remainder of [6(x+1)] when divided by (x^2 + 3x - 4). Find the values of a and b.

ANS: x^2 + 3x -4 can be factorised (cross method, formula, graphical method or remainder theorem) into (x+4)(x-1)
Thus x= -4 or 1

f(x) = ax^3 - 9x^2 + 7x + b
Let f(-4) = -64a + b -172
Let f(1) = a+b-2

if the remainder is 6(x+1)
-64a+b-172=-18

a+b-2=12
a=14-b
If we sub a with (14-b)

-64(14-b)+b = 154
=-896+65b=154
65b=1050
b= 16/2/13

a+16/2/3 -2 = 12
a= -2/2/13

Factorisation of quadratic equations
eg. x^2-6x+8

Cross method
x    -2  -2x
x    -4  -4x
_______
X^2 +8 -6x

(x-2)(x-4)

Formula [b+sqrt(-b^2-4(a)(c)]/2(a)
[-(-6)+sqrt((-6)^2 - 4(1)(8)] / 2(1)
[6+sqrt(36-32)]/2 = 2 or 4

Remainder Theorem
if (x-2)=0, x=2 [Guess and Check)
f(x) = x^2-6x+8
f(2) = 2^2-6(2)+8
     = 0
If there is no remainder it means that (x-2) is a factor.

21th Jan

Authentic Assessment using ICT


1:identify a polynomial
2:perform long division
3:perform synthetic division
4:solve cubic equation.


o(∩_∩)o ：do remember to write and organize clear and necessary explanation and do pay attention to your handwriting,it is very important for your O level tests.

18 Jan lesson's summary

worksheet A01C Q6

1       

                     1   2   1

                 1   3     3   1

              1   4     6    4    1

          1    5   10    10   5     1

Binomial

(a+b)^1=a+b

(a+b)^2=a^2+2ab+b^2

(a+b)^3=a^3+3a^2b+3a^1b^2+b^3

(a+b)^4=a^4+4a^3b^1+6a^2b^2+4a^1b^3+b^4

(a+b)^5=a^5+5a^4b^1+10a^3b^2+10a^2b^3+5a^1b^4+b^5

Linear

y=mx+c

m-gradient(slope)

c-y-intercept

Quadratic

Y=ax^2+bx+c

Roots:

Real & equal:

Real & distinct:

Imaginary:

Cubic:

3 kinds of graph 

h(x) = x³ - 4

f(x) = x³ + 4x² + 3x + 1

g(x) = x³ + x

Sorry for posting it late.

 Done by Crystal

PARTIAL FRACTION

BY MR JOHARI

A. Introduction to PARTIAL FRACTIONS

RESOURCE: PARTIAL FRACTIONS

TOWARDS DISTINCTION - QUIZ

BY MR JOHARI

Please attempt the following Topics/Questions from ACE Learning Maths Portal.

URL:  http://www.ace-learning.com/index.php

For first time User: 

Username: NRIC 

Password:  NRIC

[Please inform your Maths Teacher should you encounter any problem]

Task: Compulsory

Complete the following on-line Quizzes. Advice: Review topic(s) before attempting the Quiz(zes)

Quiz 1:Polynomials - Identity

Quiz 2:Remainder Theorem

Quiz 3:Factor Theorem

Must be attempted by end of Week 3. Marks will be recorded and reviewed. 

All the besr.

17 Jan Lesson summary

Explanation for Homework

-A01B Question4

Given that x^3+7x^2+ax-5=(x^2+x-2)f(x)+(x-1)(bx-1), find

 a)the value of a and of b
 b)f(x).

-Solution
a)
x^3+7x^2+ax-5=(x^2+x-2)f(x)+(x-1)(bx-1)
                     =(x-1)(x+2)f(x)+(x-1)(bx-1)
   if x=1, 
  1^3+7*1^2+1*a-5 = 0*(1+2)f(x)+0*(bx-1)
   3+7+a-5=0
   so a=-3
   if x=-2, 
  (-2)^3+7*(-2)^2+(-2)*(-3)-5=(-2-1)*0*f(x)+(-2-1)(-2b-1)
  -8+28+6-5=0+6b+3
   so b=3
b)
∵a=-3 b=3
∴x^3+7x^2+(-3)x-5=(x^2+x-2)f(x)+(x-1)(3x-1)
   x^3+7x^2+(-3)x-5=(x^2+x-2)f(x)+(x-1)(3x-1)
   
   f(x)= x^3+7x^2+(-3)x-5 - (x-1)(3x-1)
                     x^2+x-2
        
        =
Explanation
A)  identity means it's true for all values of X
No matter what x is, LHS=RHS

when the main problem of Q4 is we don't know f(x), we can make x=1or -2, to make f(x)multiply zero and help us find the value of a and b.

B)Actually, 
x^3+7x^2+(-3)x-5 is like the Dividend
(x-1)(3x-1) is like the remainder
x^2+x-2 is like divisor
f(x) is like quotient

Remainder Theorem

3methods to find the remainder
M1:Traditional division(on P45)
M2:Synthetic division
M3: make the divisor(at the bottom) become zero and get that value of x
      put that value in the dividend
      if the result is zero, it means no remainder and this is FACTOR THEOREM
      if the result is other numbers, that is the remainder and this is REMAINDER THEOREM

Division - Long Division to Remainder Theorem

Please go the the following link and summarise the content as follows:

• What is the overall understanding that the author is trying to explicate from the explanation.
• What are the key concepts of Mathematics - Remainder Theorem that the author is emphasizing?
• If you are required to explain the linkages between Long Division, Synthetic Division and Remainder Theorem, how would you do it?

Work in groups not more than 3 and post it as a new entry.

Title: Division (exploration)

done by:  (group members' names)

Label: Polynomial


Time given: 15minutes.

16/1/12 Lesson Summary

By Jemima

Remainder Theorem
- Used to find the remainder
- 0 isn't a remainder, if you get a 0, it would be factor theorem

Worksheet A01B (Polynomials)
Question 1: State whether the function is a polynomial, then explain why or why not

Question 2: Exapnd whenever necessary
                   There are 2 methods that can be used to solve the questions
Method 1
2x^2+3x≣(A-2)x^2+(B-1)x
2=A-2          3=B-1
A=4             B=4

or

Method 2
If x=1
5=A-2+B-1
A+B=8

Question 3: for (b) and (c) is not an identity.
                    The way to write the conclusion: Since there are multiple values of A, B and C, ∴the
                    above is not an identity.

Question 4:
x^3+7x^2+ax-5 -> Dividend
(x^2+x-2) -> Divisor
f(x) -> Quotient
(x-1)(bx-1) -> Remainder

(2x^3+4x^2-5)/(x-1)(x+2)=2x+6+1/(x-1)
Sub x=1 for A; Sub x=-2 for B

f(x)=(x^3+4x^2-6)/(x+3)(x-1), x≠-2 or 1
∴ The above is not a function as an asymptote would be encountered.

Homework
- Redo Worksheet A01A (Functions)
- Read and understand the chapter on remainder theorem
- Complete practice 7 on page 52

WS A01A (FUNCTION)

15/01/2013 Lesson Summary

POLYNOMIALS

By Desiree

A polynomial in the variable x is a mathematical expression involving the sum of terms. It is in the form of ax^n, where a is a coefficient to the power of n, which has to be a non-negative number. Division by variables are not allowed.

Polynomials are arranged systematically, in acceding or descending order according to the power of x.

The degree or the degree of freedom, is the highest power in the polynomial.


When the LHS of an equation is the same as the RHS of the equation for all values of x, it is called an identity. A "≡" symbol is used.
If both expression co-incide on a graph, they are an identity. (refer to mason's post below ^^)
Polynomials will be affected by the values of x, hence, x² -1 / x-1 is not an identity of x+1. This is because x in this equation cannot equal to 1 and the definition says it has to be true for all values of x.

Note: -1³ ≠ (-1)³ , remember to insert the brackets when necessary.

DIVISION OF POLYNOMIALS

Using the primary school analogy of long division, we can gather dividend ≡ divisor x quotient + remainder.

Sometimes there will be "missing terms" (example: there may be an x³, but no x²). In that case, include the missing terms with a coefficient of zero.

http://www.mathsisfun.com/algebra/polynomials-division-long.html
http://www.purplemath.com/modules/polydiv2.htm

You also can use Synthetic Division. The divisor should be linear and the first step is to make it equal to zero to find the value of x and put it on the left side.

http://www.purplemath.com/modules/synthdiv.htm
Math book.

Lastly, you could just try to input factors to work out the remainder.

Polynomials Practice 1C

By Mason S309

Refer to Practice 01 p39

2x^2 +5x- 3A(x-B)^2 + C
2x^2 +5x- 3A^22 -2ABx+AB2 + C
Comparing coefficients
2x^2=Ax^2
A=2 A=2 , B = -1 1/4 , C = -6 1/8

5x =-2ABx
5=-4B
B=-1 1/4

-3 =AB^2 +C
-3 =3 1/8 +C
C = -6 1/8

To check if the solution is correct use a suitable graphing tool.
If the solution is correct the 2 graphs should coincide as shown below.

Picture of both equations together . ( Correct values for A , B and C )

POLYNOMIAL - DIVISION

MODEL OF DIVISION

LONG DIVISION

LONG DIVISION to SYNTHETIC DIVISION

REMAINDER THEOREM